2000年奥运田径女冠军1、王丽萍,1976年7月出生于辽宁凤城,田径运动员,奥运冠军。2、 2000年,王丽萍获得悉尼奥运会女子20公里竞走金牌,这是中国在悉尼奥运会上得到的惟一一枚田径金牌。3、 1996年,王丽萍在训练中膝伤复发,
佛罗伦萨美术学院怎么去 佛罗伦萨美术学院研究生容易毕业吗
佛罗伦萨美术学院怎么去佛罗伦萨美院作为艺术类排名世界第三大学,入学考试相对较为简单,除了可以走图兰多计划外,还可以走普通国际学生,也可以参加现在个别中介与大学联合推出的合作计划,一些大型的拥有双资质的留学中介,会有合作计划,你可以去询问一下
佛罗伦萨美术学院怎么去
佛罗伦萨美院作为艺术类排名世界第三大学,入学考试相对较为简单,除了可以走图兰多计划外,还可以走普通国际学生,也可以参加现在个别中介与大学联合推出的合作计划,一些大型的拥有双资质的留学中介,会有合作计划,你可以去询问一下。关于入学考试,只要意大利语过关,并且有一定的美术基础,入学考试就不难。
佛罗伦萨美术学院研究生容易毕业吗
1、佛罗伦萨美术学院研究生不是很容易毕业
2、佛美语言要求很严格,没有B2成绩不用想。教授年纪普遍偏大,学术性很强,原则性也很强,感情分完全没有。佛美是世界美院之母,每个去意大利的美术生,对佛美都有说不出的情感,报的学生是蛮多的,佛美的纯艺如油画是非常出名的,也是王牌专业,竞争肯定是比较大的。
相关文章
- 详细阅读
-
wlk防骑单刷破碎带什么雕文 wow防骑雕文详细阅读
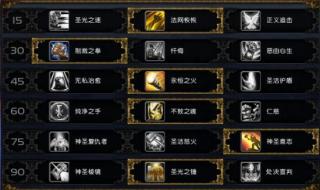
一、wlk防骑单刷破碎带什么雕文1、大型雕文:正义之锤雕文(多打一个);神圣恳求雕文(3%减伤);复仇雕文或神圣愤怒雕文。 2、小型雕文:圣疗雕文;王者雕文;感知亡灵雕文。二、335防骑用什么雕文1、大型:2、正义之锤雕文(多打一个)3、神
-
谁知道长江大桥具体选址和沿江大道路线及方案图吗 武穴长江大桥详细阅读

一、谁知道长江大桥具体选址和沿江大道路线及方案图吗出口一:梅川松阳(连接s308),出口二:四望德利桥附近(从望武公路往西连接横马线,往南连接松马线),出口三:武穴城区出口(连接武穴大道即江北一级公路)。离四望最近的两条高速相交互通但没有出
-
吸血鬼日记klaus怎么是历史老师 吸血鬼老师详细阅读
一、吸血鬼日记klaus怎么是历史老师klaus的巫师用巫术让klaus附身在了历史老师的身体上,这样就可以用历史老师的身份来探听damon他们的情报。 二、吸血鬼日记历史老师的老婆和凯瑟琳到底是不是同一个人凯瑟琳是500年前的二重身,而艾
-
世界女排联赛2022总赛程 女子排球超级联赛赛程表2021-2022详细阅读

世界女排联赛2022总赛程1、北京时间2022年7月4日凌晨,随着2022年世界女排联赛加拿大卡尔加里站最后一场比赛结束,2022年世界女排联赛总决赛参赛的八支球队也出炉。八支球队将先进行1/4决赛的争夺。单场淘汰制。美国女排,巴西女排,意
-
如果不能到永远歌词是什么意思 如果不能到永远详细阅读

一、如果不能到永远歌词是什么意思关于这个问题,这首歌的主题是关于远距离恋爱的挑战和困难。歌词中表达了无法经常见面和相处的痛苦,同时也表达了对爱情的坚持和承诺。如果不能到永远,意味着他们无法保证永远在一起,但他们仍然会尽力维持这段爱情。二、如
-
过道吊顶要多高最合适 家装过道吊顶效果图详细阅读

一、过道吊顶要多高最合适1.过道吊顶高度多少合适 对于过道吊顶的高度,并没有一个准确的数值。通常情况下,过道吊顶高度应不少于2.4米,如果条件允许,高度是越高越好的。但是具体的高度还是要根据现场情况来定的,具有可调节性。另外,过道吊顶的高度
-
2010冬奥会中国第一金的获得者是谁 2010冬奥男单冠军详细阅读

2010冬奥会中国第一金的获得者是谁1、申雪/赵宏博 。在温哥华冬奥会双人滑比赛中,中国选手申雪/赵宏博以216.57分的总成绩夺得冠军。这是2010年温哥华冬奥会中国代表团获得的第一块金牌。改写了中国花样滑冰冬奥会无金牌的历史。2、另一对
-
lpl春季赛赛程2022何时开始 2022年世界杯赛程表及结果详细阅读

lpl春季赛赛程2022何时开始1、答:2021年lpl春季赛的开始时间将会在1月10日,揭幕战很有可能是ig对阵任何一个队伍。2、LPL春季赛一般会有9周的时间,当然还会有两周的春假,所以各大战队也是会改变自己的阵容。3、本赛季FPX几乎
-
山东男篮赛程时间表2020-2021 辽宁篮球比赛赛程表2021至2022详细阅读

山东男篮赛程时间表2020-20211、2020-2021赛季CBA联赛将于10月17日正式打响,日前,CBA官方公布了常规赛第一阶段的赛程。CBA新赛季将在10月17日开赛,进行至11月14日,各支球队将在诸暨征战12轮常规赛。2、其中,
-
韦东奕的数学成就国际认可吗 韦东奕国际数学排名详细阅读

一、韦东奕的数学成就国际认可吗1、认可。2、韦东奕在三维纳维一斯托克斯方程正则性问题和二维不可压缩欧拉方程的线性阻尼问题上,取得了一系列重要研究进展 。他还与人合作在随机矩阵理论研究中取得重大成果。截至2019年12月,韦东奕已在国际数学期
